前文講:R-squared 不代表一切,似乎有點太令人驚訝,得到許多網友的反饋。很抱歉造成這些困擾,我應該把文章一次發完的。無奈最近有太多稿子在寫了,每篇文章都得分好幾次才能寫完。
R-squared 不代表一切,那究竟什麼重要呢?準確地分析才是重點。參考文獻這篇文章:Does Head Start make a difference? 提供了很好的範例,我簡單呈現給大家看看。這篇文章跟我的領域不是有很大的關係,我就懶得弄書目了,反正連結裡面的pdf檔有大家要的資訊。
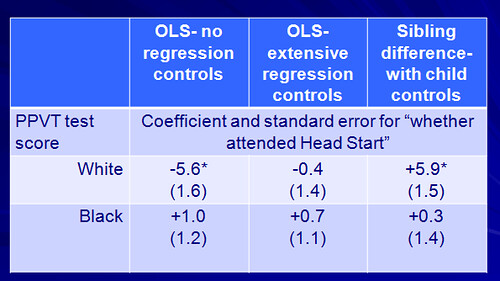
簡單地說,這篇文章在看一個 program (你也可以想成是intervention如果這樣比較容易的話) 是否對學生的學習成就有影響。這篇的重點可以用下面的圖來表示 (原數據可見參考文獻pdf的第14頁或p352)。
PPVT 是學生的學習成就。第一欄是 OLS,不加任何控制變量,你會看到這個 program 降低了白人的學習成就,對黑人來說是有所助益的,但結果並不顯著。第二欄是 OLS 加上一堆控制變量,你看到這個 program 現在看起來,對白人與黑人是差不多的,都沒有顯著差異。
看到這裡,問題還沒結束。你心裡應該想著:那這些人是怎麼選進這個 program 的?會不會是否進這個 program 就已經存在著差異,即使我們控制了這麼多變數呢?這些 unobserved variables 是否會影響到我們的結果?那如何作才能獲得更準確地估計呢?
由於家庭內有太多變量可能會影響到家長是否送小孩到這個 program,我們又沒辦法控制所有的變數,於是經濟學家想出了一個方法:fixed effect,利用固定效應來控制這些無法觀察到的變數。
用簡單一點的語言來說,如果一個家裡有兩個小孩,一個送到這個program,一個沒送到這個program,這兩個小孩之間的差異,其實就會抵消了 unobserved variable 的影響。更嚴格地說,會影響到家長送小孩到這個 program 的因素中,如果這些因素是持續不容易改變的話,那這些因素就會被控制住了。換言之,unobserved time-invariant mother/famility effect 就不需要擔心了。我不愛寫公式,但如果愛看公式可以看下面的:
小孩1學習成就 = a0 + b1 * Head Start + b2 * 家庭因素 + b3 *小孩1的特定變數
小孩2學習成就 = a1 + b4 * head Start + b2 * 家庭因素 + b5 *小孩2的特定變數
這兩條公式相減,就可以抵消這些持續不變的家庭因素,對家長是否送小孩到這個 program 的影響,從而可讓 head start 是否對小孩學習成就的估計更加準確。
看看上面的結果,第三欄採用了 mother fixed effect, 結果就完全翻盤了,這個 program 提高了白人的學習成就,但卻未提高黑人的成就。所以雖然一開始你得到了顯著差異,但你更要關心的是:我的估計是否準確?是否有其它的東西我並未控制?是否有 unobserved variables,我可以用什麼方式控制 unobserved variabes。
參考文獻
Does Head Start make a difference?
標籤: 統計分析