圖中???的地方,就是你不知道的,也就是我們上面所說的latent variable或factor。意思是:???你沒有辦法直接觀察,但你可以藉x1、x2、x3來間接得知???。太抽象了?那用實際點例子,你想知道「快樂」,但你沒有辦法直接看一個人就知道他快不快樂,所以你可以用其它的方式,像「每日笑的次數」、「外出旅遊次數」、「朋友數」來知道他是否快樂(好像例子不是很好 @@)。
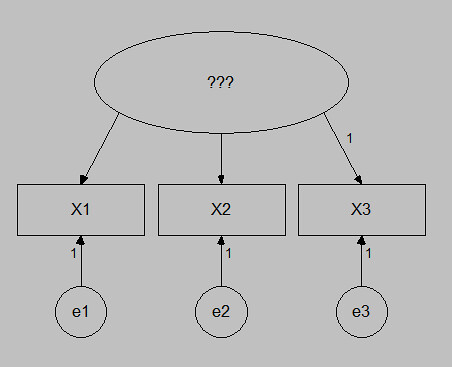
這裡要講的因素分析不是在ANOVA裡面看到的Factor Analysis of Variance,而是結構方程模式分析(Structural equation model,簡稱SEM)裡面的一環。因素分析裡面一定會有latent variable(隱性變量),又有人稱為factors(因素)。講半天還是不知道是什麼,對吧?有圖有真相:

圖中???的地方,就是你不知道的,也就是我們上面所說的latent variable或factor。意思是:???你沒有辦法直接觀察,但你可以藉x1、x2、x3來間接得知???。太抽象了?那用實際點例子,你想知道「快樂」,但你沒有辦法直接看一個人就知道他快不快樂,所以你可以用其它的方式,像「每日笑的次數」、「外出旅遊次數」、「朋友數」來知道他是否快樂(好像例子不是很好 @@)。
當然你也可以換個角度來想factor analysis。你有了一堆變數,你覺得有某幾個變數組合起來,可以用一個或少數抽象觀念(construct)來表示,這就是factor analysis所處理的事。如果要講的「統計」一點,就是:你可以用一個或少數的factor,解釋x1、x2、x3這些可觀察到行為的差異。
為什麼要作這樣的事?簡單地說,目的就是減少變數,而減少變數的好處,是可以讓你的整個model看起來更清楚。我們可以看看這篇經典的文章:The mechanism mediating the effects of poverty on children's intellectual development。下面是這篇文章的圖二。
這篇文章想要探討貧窮(最左上角)與智能發展(最右邊方框)的關係。我們看最上面的一個橢圓型,裡面寫Cognitive stimulation(認知刺激)。橢圓型在結構方程模式分析表示的就是latent variable或factor,而這個因素是從y9-y13得到的,分別是書、雜誌、母親對小孩閱讀、Record or tape、博物館參觀。由這五個因素我們可以用factor analysis得到一個抽象的概念:cognitive stimulation(你會得到一個東西,至於這個東西是什麼,要靠你自己想或「建構」),這樣一來,poverty 與 cognitive stimulation的因果關係就很清楚了,你也可以看到cognitive stimulation與intellectual development的因果關係。如果不用factor analysis,而是將y9-y13放進這個model,得到的結果一定沒這麼漂亮&有說服力。
總之,factor analysis是一種減少變數的方法,而得到的這變數可以用於SEM中或是與其它的變數再做regression。至於為什麼知道幾個變數可以得到一個或數個factor,甚至給這個factor一個數值,這是複雜的數學與統計,想知道的就去查書或問你的統計老師吧!
如果你想要知道更多關於Factor analysis,可以參閱此網頁:http://faculty.chass.ncsu.edu/garson/PA765/factor.htm
標籤: 統計分析